第3回: 競馬予測 AI: ロジスティック回帰
前回の振り返り
前回の記事では、競馬のレースデータを機械学習モデルが理解できる形に変換しました。
- 文字列データを数値に変換(タイム、体重、性齢など)
- 特徴量エンジニアリング(前走成績、騎手の平均着順など)
- One-Hot Encoding でカテゴリ変数を数値化
- 日付の周期性を sin/cos で表現
前処理済みのデータが手元にあるのでいよいよ AI モデルの構築です。
- 機械学習の基本フロー(学習・推論・評価)を理解する
- ロジスティック回帰モデルで「3着以内に入るかどうか」を予測する
- モデルの性能を正しく評価する方法を学ぶ
- どの特徴量が重要かを可視化して解釈する
なぜロジスティック回帰から始めるのか
「AI」「機械学習」と聞くと、複雑な深層学習(ディープラーニング)を思い浮かべるかもしれません。でも、最初からいきなり複雑なモデルに飛びつくのは得策ではありません。なぜなら:
- シンプルなモデルで十分な場合がある
- 複雑なモデルは解釈が難しい(なぜその予測になったか分からない)
- ベースラインとして、後のモデルと比較するための基準が必要
ロジスティック回帰は「線形モデル」と呼ばれる最もシンプルな分類モデルの一つ。解釈しやすく、「AI がどの要素を重視しているか」が一目で分かるのが大きなメリットです。
「まずはシンプルに」の精神
実務でも「まずロジスティック回帰でベースラインを作り、それを上回れるか」という形で複雑なモデルの価値を評価することが多いです。いきなりディープラーニングを使って「なんとなく動いてる」状態より、シンプルなモデルで仕組みを理解することが大切です。
ロジスティック回帰の仕組み
コードを書く前に、ロジスティック回帰がどうやって予測を行うのか理解しておきましょう。
決定境界で分類する
ロジスティック回帰は、データを「決定境界(Decision Boundary)」で 2 つのグループに分けるモデルです。
下の図は、2 つの特徴量を使って分類するイメージです:
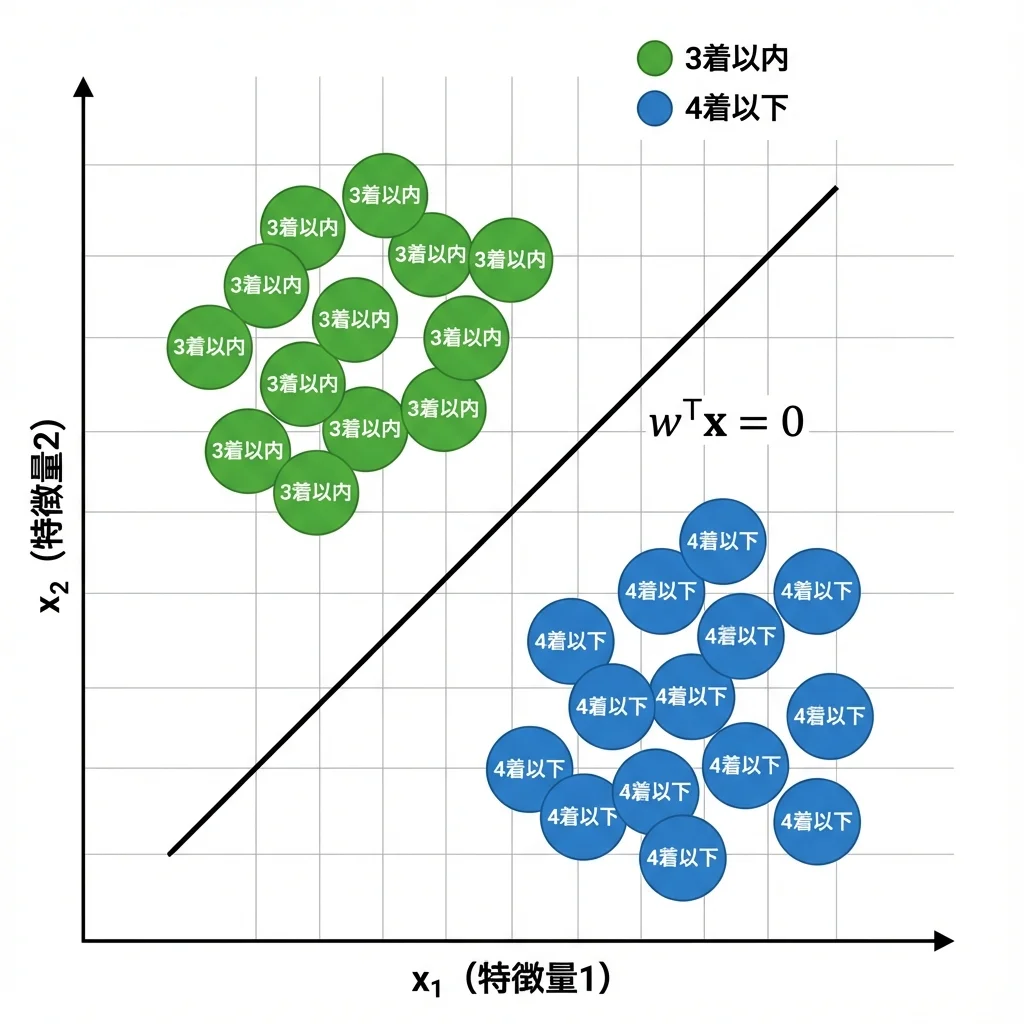
- 緑の点:「3 着以内」に入るグループ
- 青の点:「4 着以下」のグループ
- 直線:決定境界
ロジスティック回帰は、この 2 つのグループを最もきれいに分ける直線を自動的に見つけます。
シグモイド関数で確率を出力
実際には「0 か 1 か」ではなく、「3 着以内に入る確率」を出力します。この時に使うのがシグモイド関数です。
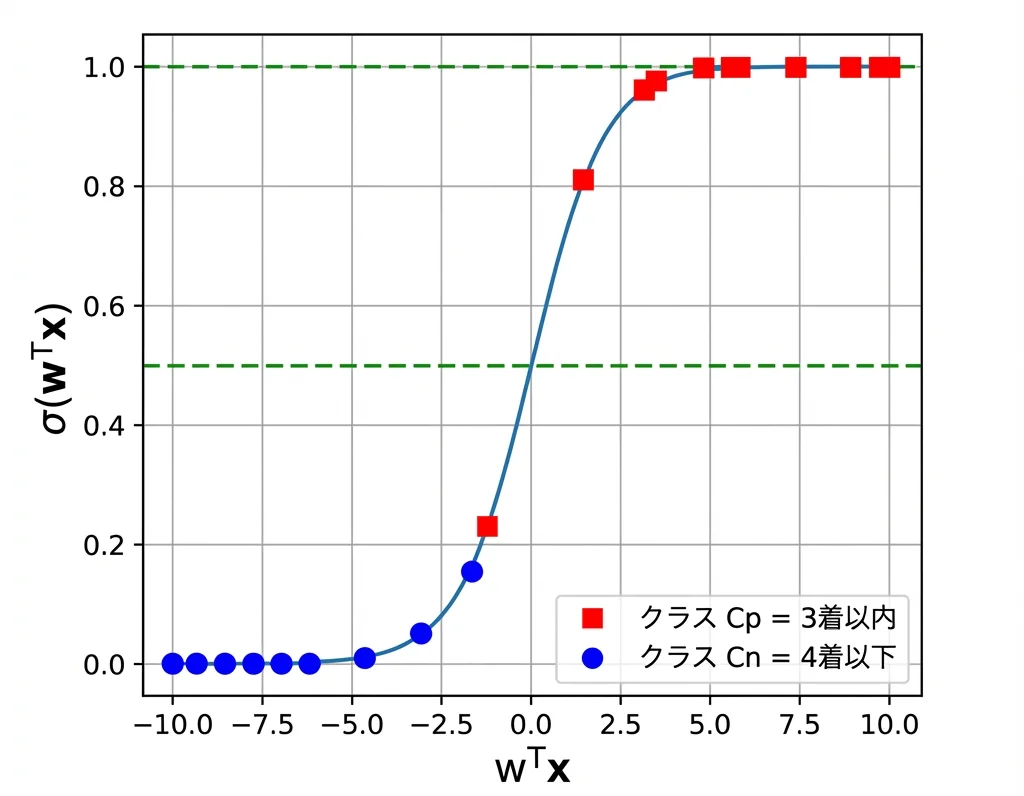
- wx が大きい → 確率は 1 に近づく(「3 着以内」の可能性が高い)
- wx が小さい → 確率は 0 に近づく(「4 着以下」の可能性が高い)
- wx = 0(境界線上) → 確率はちょうど 0.5
重み w が大きい特徴量ほど、予測に大きな影響を与えます。後でこの重みを可視化して、AI が何を見ているかを確認します。
機械学習の基本フロー
機械学習の基本的な流れを押さえておきましょう。
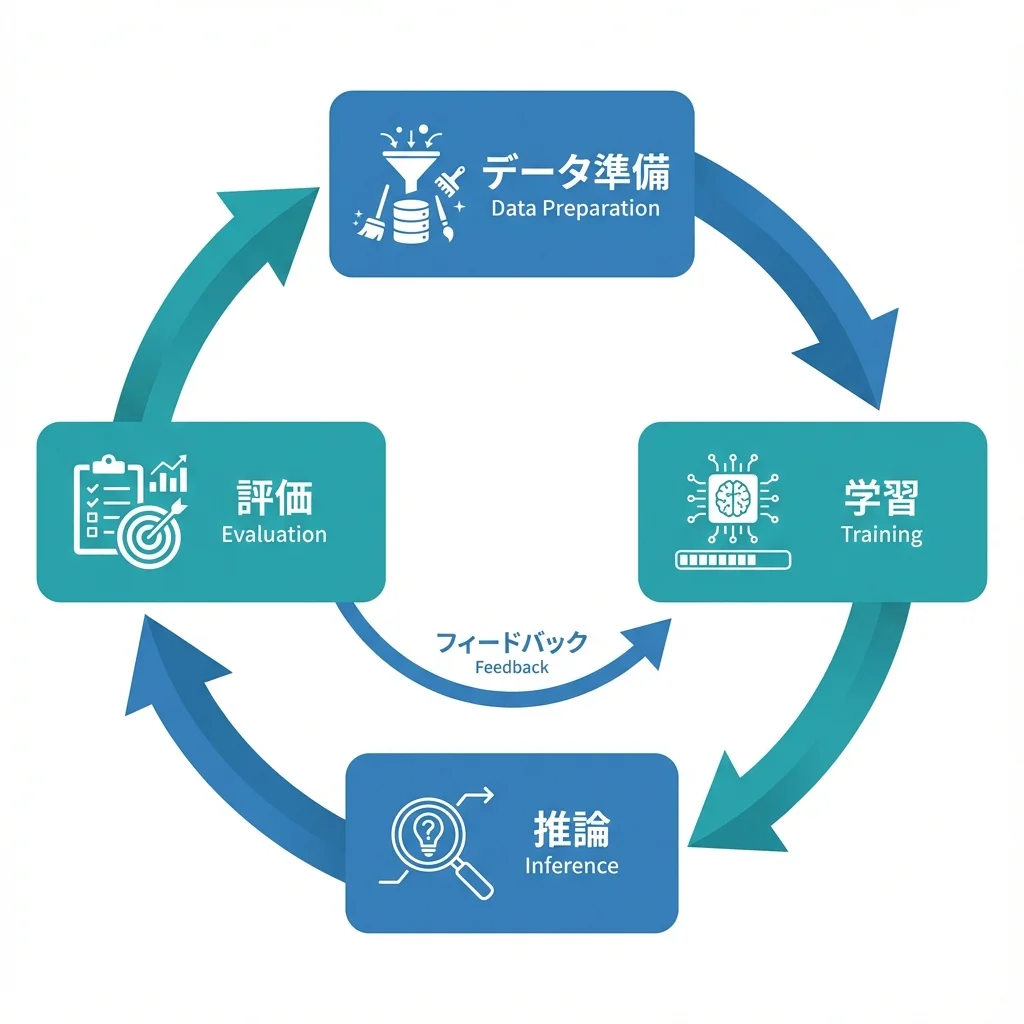
- データ準備: 前回までの作業。モデルに入力できる形にデータを整える
- 学習(Training): データを使ってモデルにパターンを覚えさせる
- 推論(Inference): 学習したモデルで未知のデータを予測する
- 評価(Evaluation): 予測がどれくらい当たっているかを検証する
なぜデータを分割するのか
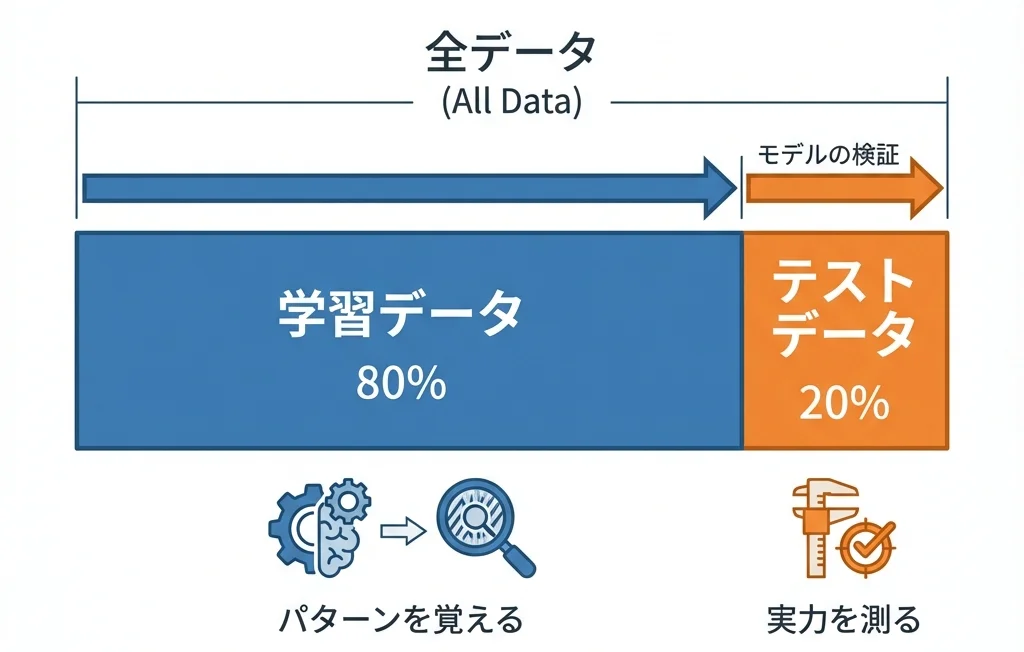
ここで重要なのが「学習データ」と「テストデータ」の分割です。
学校のテストで、先生が「事前に問題を教えるね」と言ったらどうでしょう。みんな 100 点を取れますが、それは本当の実力でしょうか?
機械学習でも同じです。学習に使ったデータで評価すると、モデルは「答えを丸暗記」しているだけかもしれません。本当の実力を測るには、学習に使っていない「初見」のデータで評価する必要があります。
実装してみよう
環境準備
まずは必要なライブラリをインポートします。
!pip install japanize-matplotlib
from google.colab import drive
import numpy as np
import pandas as pd
import os
import warnings
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.impute import SimpleImputer
from sklearn.metrics import accuracy_score, f1_score, classification_report
drive.mount("/content/drive")
BASE_DIR = "drive/MyDrive"
warnings.simplefilter("ignore")sklearnは Python で最も広く使われている機械学習ライブラリです。
データの読み込み
前回保存した前処理済みデータを読み込みます。
df = pd.read_csv(os.path.join(BASE_DIR, "processed_all_result.csv"))
print(f"データ件数: {len(df)} 行, {len(df.columns)} 列")
df.head()目的変数と説明変数の準備
今回予測するのは「3 着以内に入るかどうか」です。なぜ「1 着」ではなく「3 着以内」なのか?複勝という馬券形式があり、的中率と回収率のバランスが取りやすいからです。
# 目的変数の作成
df["target"] = (df["着 順"] <= 3).astype(int)
# 予測に使えない情報を除外
exclude_cols = ["着 順", "target", "人 気", "タイム"]
feature_cols = [c for c in df.columns if c not in exclude_cols]
X = df[feature_cols]
y = df["target"]
print(f"説明変数: {X.shape[1]} 個")
print(f"目的変数の分布:\n{y.value_counts(normalize=True)}")人気やオッズは使わない!
「人気」や「オッズ」を入れると精度が上がりますが、これらは「予測結果そのもの」に近い情報です。私たちが知りたいのは「他の人が気づいていない穴馬」なので、人気の情報は使いません。
欠損値の処理
新馬戦に出走する馬には「前走着順」がないなど、実際のデータには欠損値があります。
imputer = SimpleImputer(strategy="mean")
X_imputed = imputer.fit_transform(X)
print(f"欠損値処理前: {X.isnull().sum().sum()} 個")
print(f"欠損値処理後: {np.isnan(X_imputed).sum()} 個")データの分割
X_train, X_test, y_train, y_test = train_test_split(
X_imputed, y,
test_size=0.2, # 20%をテスト用に
random_state=42 # 再現性のためシード固定
)
print(f"学習データ: {len(X_train)} 件")
print(f"テストデータ: {len(X_test)} 件")モデルの学習
model = LogisticRegression(max_iter=1000, random_state=42)
model.fit(X_train, y_train)
print("学習完了!")fit() メソッドでモデルが最適な重み w を自動計算してくれます。
交差検証
1 回だけの評価では、たまたま良い(または悪い)データ分割だったかもしれません。交差検証で安定した評価を行います。
cv_scores = cross_val_score(model, X_imputed, y, cv=5, scoring="accuracy")
print(f"交差検証スコア: {cv_scores}")
print(f"平均スコア: {cv_scores.mean():.4f} (±{cv_scores.std():.4f})")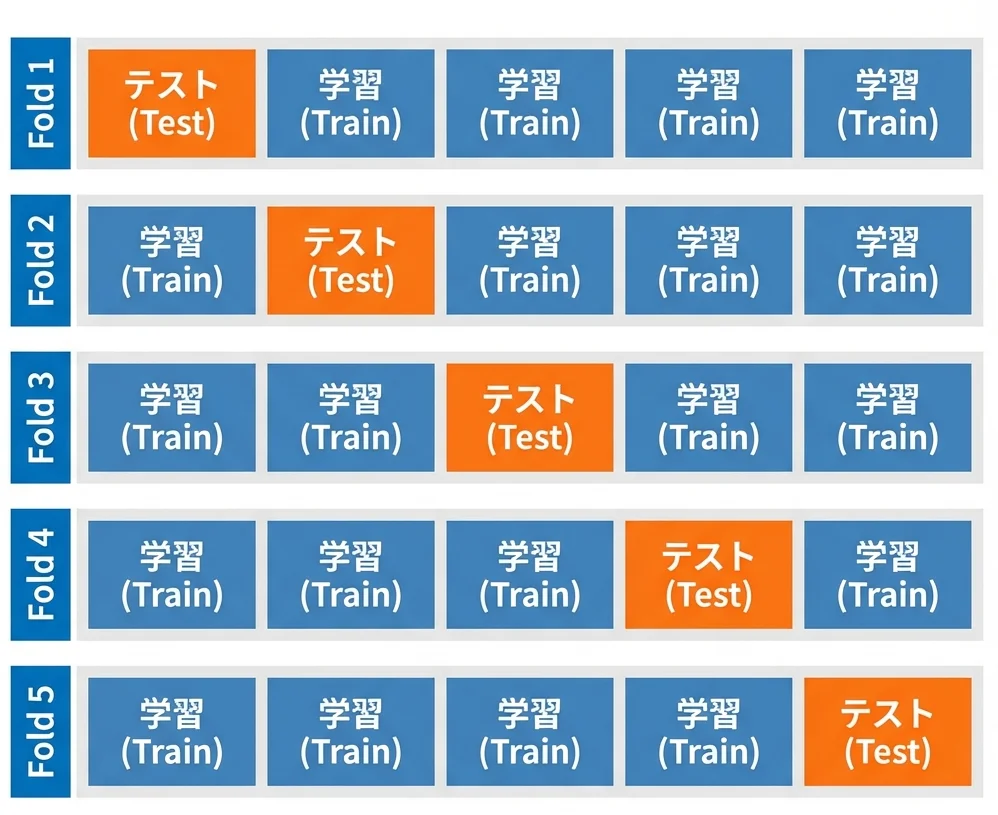
データを 5 分割し、それぞれを順番にテストデータとして使います。5 回分の結果を平均することで、より信頼性の高い評価ができます。
テストデータでの評価
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print(f"正解率 (Accuracy): {accuracy:.4f}")
print(f"F1スコア: {f1:.4f}")
print(classification_report(y_test, y_pred, target_names=["4着以下", "3着以内"]))結果の解釈
期待される結果
実行すると、おおよそ以下のような結果が得られます:
平均Accuracy: 0.78〜0.79
平均F1 Score: 0.17〜0.18
Test Accuracy: 0.79
Test F1: 0.18「Accuracy は 78% もあるのに、F1 は 18% しかない…?」
この差こそが重要なポイントです。
正解率だけを見てはいけない理由
競馬では 3 着以内に入る馬は全体の約 17〜30%。つまり、すべて「4 着以下」と予測するだけでも正解率 70% になります。
今回のモデルは「4 着以下」を正確に予測できていますが、肝心の「3 着以内」を見つける力(F1 スコア)はまだ発展途上です。
係数の可視化
ロジスティック回帰の強みは、どの特徴量が重要かが分かること。
coefficients = model.coef_[0]
coef_df = pd.DataFrame({
"feature": feature_cols,
"coefficient": coefficients
})
# 騎手のダミー変数を除外してソート
coef_df_filtered = coef_df[~coef_df["feature"].str.startswith("騎手_")]
coef_df_sorted = coef_df_filtered.reindex(
coef_df_filtered["coefficient"].abs().sort_values(ascending=False).index
)
top_features = coef_df_sorted.head(15)
# 可視化
plt.figure(figsize=(10, 8))
colors = ["#2ecc71" if x > 0 else "#e74c3c" for x in top_features["coefficient"]]
plt.barh(top_features["feature"], top_features["coefficient"], color=colors)
plt.xlabel("係数")
plt.title("ロジスティック回帰の係数(騎手除く)")
plt.gca().invert_yaxis()
plt.tight_layout()
plt.show()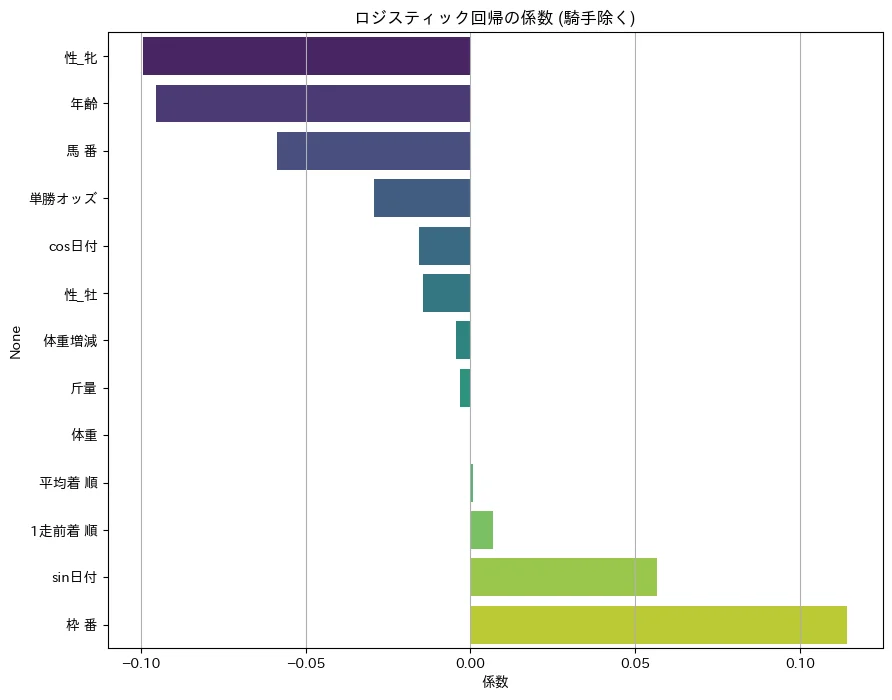
グラフの読み方:
- 正の係数(右側): 値が大きいほど「3 着以内」に入りやすい
- 負の係数(左側): 値が大きいほど「3 着以内」に入りにくい
この結果から分かること:
- 枠 番(正): 外枠の馬ほど好走しやすい傾向
- sin 日付(正): 季節性の影響
- 性_牝(負): 牝馬は 3 着以内に入りにくい傾向
- 年齢(負): 高齢馬ほど 3 着以内に入りにくい
係数の解釈には注意も必要です。特徴量のスケールが異なると、係数の大きさだけでは重要度を比較できません。また、直感に反する結果が出ることもあります。これは特徴量間の相関やデータの偏りが原因かもしれません。
この結果をどう見るか
F1 スコアが 0.18 という結果は、以下のことを示唆します。
- 競馬は多くの変数が絡む複雑なシステム
- プロの予想家でも的中率は 30〜40% 程度
- ランダムに選んでも 3 着以内の確率は約 17%
機械学習で何かしらのパターンを捉えられている時点で大きな一歩です。
そして重要なのは、モデルが何を見ているかが分かること。AI がブラックボックスではなく、「なぜその予測をしたのか」を説明できる。これがロジスティック回帰の最大の強みです。
まとめ
今回は、前処理したデータを使ってロジスティック回帰モデルを構築しました。
- ✅機械学習の基本フローを理解(学習 → 推論 → 評価)
- ✅データ分割の重要性(汎化性能の評価)
- ✅ロジスティック回帰モデルで 3 着以内を予測
- ✅交差検証で安定した評価
- ✅係数の可視化でモデルの解釈
「シンプルなモデルでまずベースラインを作る」という姿勢は、実際の機械学習プロジェクトでも非常に重要です。
次回は、いよいよニューラルネットワーク(深層学習) に構築します。

